How much will a baby weigh when it is born, and which babies will be unusually large? I wanted to see how well I could predict fetal birthweights, focusing on the problem of macrosomia, or large birthweight. The most common definition of this condition is that an infant weighs more than 4000 grams, or 8 lbs 13 oz at birth (though it is sometimes defined as weighing more than 4500 grams / 9 lbs 15 oz). Fetal macrosomia attracts periodic media coverage (see for example NY Times, 11 January 2016, NBC News, 16 August 2013) and is of medical concern because large infants are associated with various kinds of birth complications, including more maternal and fetal injuries at birth and more frequent hospitalization of the newborn (see Jolly et al 2003, Boulet et al 2003, Stotland et al 2004, Rossi et al 2013).
Medical providers typically rely on a combination of ultrasound and clinical exams to predict which infants will be large, but accuracy is poor and varies according to factors like who is conducting the ultrasound and the formula used to extrapolate from fetal measurements (see for example Chauhan et al 2005 and Hoopmann et al 2010). In addition, studies that examine the medical management of pregnant women suggest that providers’ success at predicting which babies will be large in practice is often even worse. One recent study based on a nationally representative survey of mothers who gave birth between 2011 and 2012 suggested that U.S. providers are wrong more than 80% of the time when they tell a woman she is likely to have a large baby, and that they only predict about 62% of actual large infants (Cheng et al 2015; see also Herrero & Fitzsimmons 1999, Sadeh-Mestechkin 2008, Phillips et al 2014).
This inaccuracy has serious costs. Because of the heightened risk of complications, ready access to hospital care is vital for women carrying large babies. For those who plan to give birth at home or who live in parts of the world where hospital birth is less common, this access could be less likely if a large fetus goes undetected. On the other hand, where hospital births are the norm, incorrectly predicting that a baby will be born large can encourage unnecessary medical interventions. In the U.S., these false positives may indeed be the bigger problem. According to the same survey mentioned above, mothers who were told they would have a large baby were more likely to have their doctor induce their labor, to try to induce labor themselves, and to have planned c-sections, regardless of the actual size of their infants (Cheng et al (2015); see also Melamed et al 2010).
In light of these issues, I wanted to explore the potential for forecasting fetal macrosomia with a different kind of predictive model. I focused on demographic and pregnancy-specific information that can be obtained without an ultrasound or physical palpation, or used in combination with these methods to inform birthweight predictions. Several studies have taken this approach before (Nahum & Stanislaw 2002, Nahum, Pham, & Stanislaw 2004, Nahum & Stanislaw 2007. However, they relied on limited samples of exclusively Caucasian women, and used only linear models to generate birthweight predictions. I aimed to see whether alternate models known for their predictive accuracy, such as random forests and gradient boosted regression, could help improve the accuracy of this kind of approach. I also wanted to see whether such a model could be applied effectively to a larger and more diverse population.
My data came from the National Center for Health Statistics, which publishes detailed records on nearly all U.S. births based on information collected by the states in the process of drawing up birth certificates. I used the records from 2014 and 2015. Following the above-mentioned studies, I focused on about 5.2 million births of single, live babies delivered at full term (37 weeks or later), without congenital anomalies or major maternal risk factors like diabetes, hypertension, or smoking during pregnancy. The target variable was birthweight in grams, and its average value was 3403. The standard deviation was 449, and 9% of these babies weighed more than 4000 grams.
I began by considering a wide variety of features. They included a number of variables that had been previously identified as important, but also some others not accounted for in existing studies. While I wanted to maximize accuracy, because the practical difficulty of applying a birthweight prediction equation increases with each additional feature, it was also important to exclude variables that add little predictive value. Ultimately, I included 9 of the most important features:
- Mother’s weight at delivery
- Mother’s pre-pregnancy body mass index
- Mother’s total weight gain during pregnancy
- Length of the pregnancy in weeks
- Mother’s race
- Number of previous births to the mother
- Mother’s age
- Mother’s education level
- Sex of the infant
There were some significant limitations to several of these variables. Those that refer to the mother’s weight and height – the top three – are all self-reported and thus noisier than they would be if measured by a medical professional at the beginning and end of a woman’s pregnancy. The data also include only the total amount of weight the mother gained during her pregnancy, although previous research (the above-mentioned studies by Nahum & Stanislaw) suggests that more frequent measurements would likely yield better accuracy. Further, the length of the pregnancy is measured in whole weeks even though babies grow rapidly in the final weeks before they are born. For instance, in these data, average birthweight for babies born at 42 weeks is more than 700 grams greater than for those born at 37 weeks (an increase of about 1.5 standard deviations). Estimating gestation in days would likely allow for greater accuracy.
Considering these limitations, I was able to predict birthweights and fetal macrosomia surprisingly well. The best results on out-of-sample data came from gradient boosted regression (xgboost), though a random forest model was nearly as good. For the best model, the average predicted birthweight was within 300 grams, or 9%, of the true value. Also, 64% of the predicted values were within 10% of the true birthweight, and 83% were within 15%.
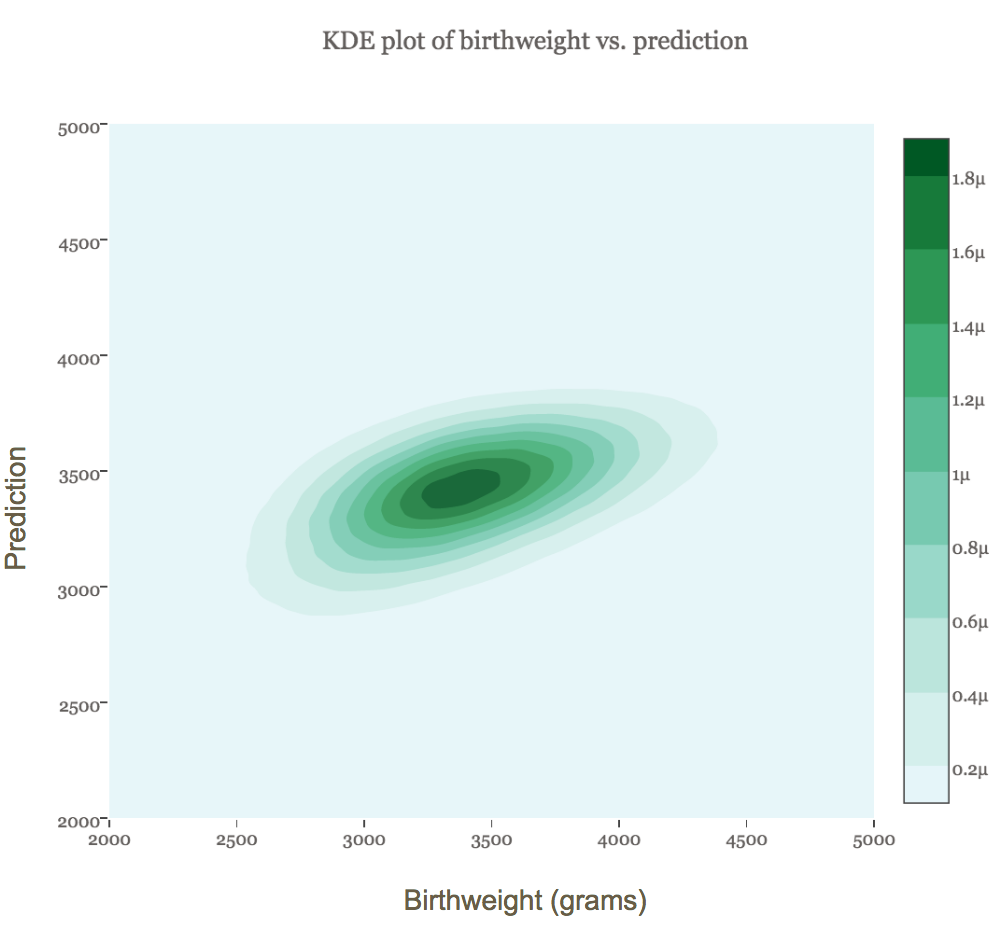
The figure below shows a kernel density plot of the joint distribution of the true and predicted values. The more darkly shaded an area is, the more observations it contains. We can see that the model was remarkably accurate for the vast majority of babies weighing between about 2500 and 4500 grams.
Translating the results into binary predictions allows us to see how the model does at predicting large babies, and to compare it with other studies. My model achieved an AUC of .77, and the receiver operating curve (ROC) is shown in the figure below. Unsurprisingly, this is not as accurate as similar studies that had access to mothers during their pregnancies and that did not suffer from the data limitations noted above. For example, Nahum & Stanislaw (2002) achieved an AUC of .83 with the average birthweight prediction within 8.1% (280 grams) of the true value. Likewise, while my model predicts macrosomia better than most of the commonly used weight estimation formulas based on ultrasound technology, a few are substantially more accurate (see Hoopmann et al 2010).
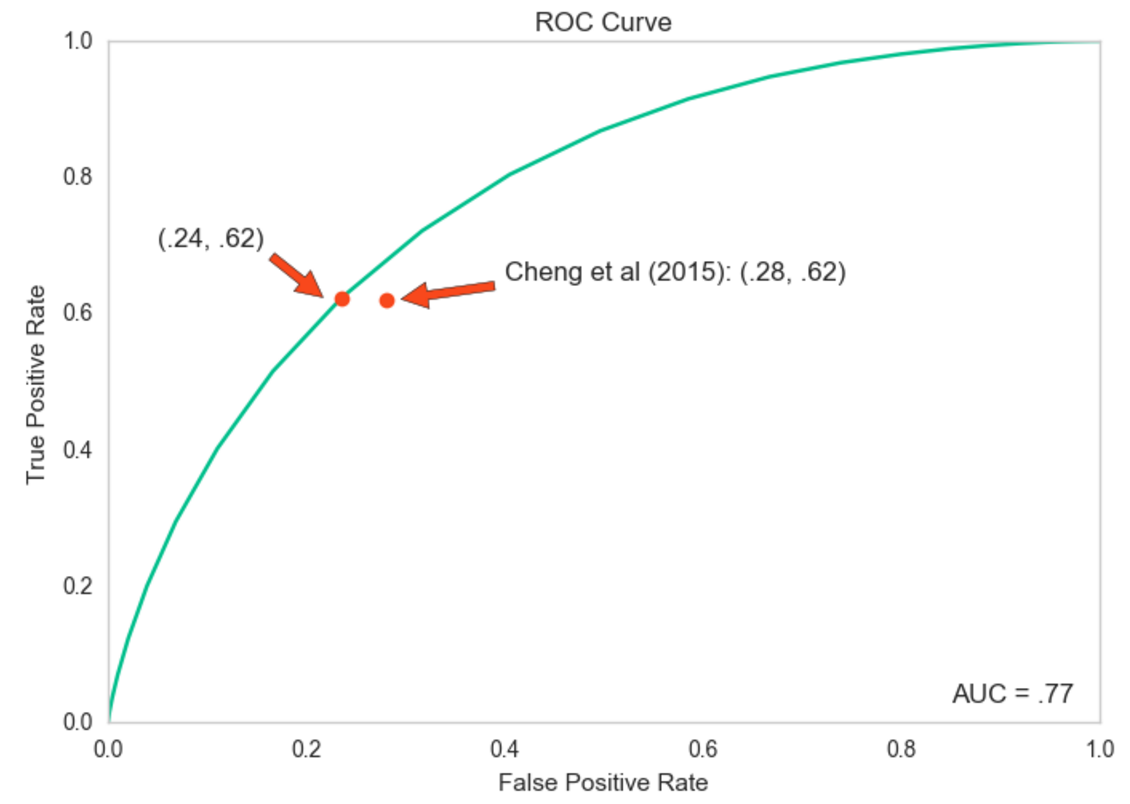
Still, perhaps the most noteworthy comparison is with the results actually achieved by the U.S. medical system, which deals with the same large, diverse population represented in the NCHS data and where not all mothers are closely tracked throughout their pregnancies. This comparison is represented by the two red dots on the above graph of the ROC curve. The dot on the left, along the curve, comes from my model: for a true positive rate of about .62 (the portion of true large babies correctly identified), there is about a .24 false positive rate (normal-sized babies incorrectly predicted as large). The other dot is calculated based on the results of the nationally representative survey of U.S. mothers presented by Cheng et al (2015). They suggest that while medical providers also correctly predict about 62% of large babies, this comes with a higher false positive rate of .28. If these results are indeed an accurate representation of American mothers’ experiences, they indicate that my model is slightly better at predicting which babies will be large than U.S. medical providers on the whole are today.
There are several interesting points to take away from this project. First, it suggests the potential to improve birthweight predictions based on demographic and pregnancy-specific characteristics by using the most effective modeling techniques. Both random forest and boosted tree regression performed better on the NCHS data than linear regression, and might do the same with the sort of data used by the other studies discussed above. Second, my results provide evidence that this kind of model can be applied effectively to a large and racially diverse population without significant loss of predictive power. Running the model on women of all races and including maternal race as a feature yielded results that were nearly identical to running the model on Caucasian women only.
More broadly, these results may help contribute to existing debates about the utility of this kind of approach to birthweight prediction. While clinical palpation is subjective, ultrasound estimates are not only often off, but are expensive and used inconsistently in practice (only about 2/3 of mothers in the Cheng at al study reported an ultrasound near the end of their pregnancy to estimate fetal weight). If existing birthweight prediction models based on demographic and pregnancy-related characteristics could be improved through the modeling techniques I applied and extended to a diverse population by incorporating information on maternal race (at least for low-risk, term births), the case for incorporating them into routine prenatal care would strengthen. One potential use could be to help identify mothers at high risk of delivering large infants earlier in their pregnancies, whether to find those in need of further screening or to suggest behavioral modifications to reduce the odds of macrosomia. At the least, my results suggest that the potential to reduce false positives deserves further investigation.
